Golang ECDHThe ECDH (Elliptic Curve Diffie Hellman) method allows Bob and Alice to share a secret. With this Bob and Alice share their elliptic curve public key for a session, and then derive the same shared key. |
Outline
A fundamental part of creating a secure tunnel - such as with HTTPs - is that the client and server generate the same shared symmetric key (typically with the AES method), and that they use this to encrypt the data passed.
In days of old, the HTTPs key exchange method was the horrible RSA encryption technique. With this, the RSA public key of the server - and which was contained on the digital certificate passed from the server to the client - was used to encrypt the session key to be used and send back the server. The server then decrypted this with its private key. The client and the server then have the same shared encryption key. But this method has a major fault … if someone discovers the private key of the server, they can decrypt all of the secret communications.
And, so, with TLS 1.3, the old public key encryption method of key exchange has been dumped, and the only show in town is ECDH (Elliptic Curve Diffie Hellman). Why? Because only the client and the server know the key used. Once the session is finished, the key is gone, and a new one is created for the next session.
package main
import (
"crypto/ecdsa"
"crypto/elliptic"
"crypto/rand"
"crypto/sha256"
"fmt"
)
func main() {
fmt.Printf("--ECC Parameters--\n")
fmt.Printf(" Name: %s\n",elliptic.P256().Params().Name)
fmt.Printf(" N: %x\n",elliptic.P256().Params().N)
fmt.Printf(" P: %x\n",elliptic.P256().Params().P)
fmt.Printf(" Gx: %x\n",elliptic.P256().Params().Gx)
fmt.Printf(" Gy: %x\n",elliptic.P256().Params().Gy)
fmt.Printf(" Bitsize: %x\n\n",elliptic.P256().Params().BitSize)
priva, _ := ecdsa.GenerateKey(elliptic.P256(), rand.Reader)
privb, _ := ecdsa.GenerateKey(elliptic.P256(), rand.Reader)
puba := priva.PublicKey
pubb := privb.PublicKey
fmt.Printf("\nPrivate key (Alice) %x", priva.D)
fmt.Printf("\nPrivate key (Bob) %x\n", privb.D)
fmt.Printf("\nPublic key (Alice) (%x,%x)", puba.X,puba.Y)
fmt.Printf("\nPublic key (Bob) (%x %x)\n", pubb.X,pubb.Y)
a, _ := puba.Curve.ScalarMult(puba.X, puba.Y, privb.D.Bytes())
b, _ := pubb.Curve.ScalarMult(pubb.X, pubb.Y, priva.D.Bytes())
shared1 := sha256.Sum256(a.Bytes())
shared2 := sha256.Sum256(b.Bytes())
fmt.Printf("\nShared key (Alice) %x\n", shared1)
fmt.Printf("\nShared key (Bob) %x\n", shared2)
}
The following is a sample run. We can see we are using the P-256 elliptic curve which has a (Gx,Gy) base point and where we use the prime number P:
--ECC Parameters-- Name: P-256 N: ffffffff00000000ffffffffffffffffbce6faada7179e84f3b9cac2fc632551 P: ffffffff00000001000000000000000000000000ffffffffffffffffffffffff Gx: 6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296 Gy: 4fe342e2fe1a7f9b8ee7eb4a7c0f9e162bce33576b315ececbb6406837bf51f5 Bitsize: 100 Private key (Alice) 61ae76afdab0de91eaf5d885c1e58b7f9aa0578e1516cb62fa9b42b27367c972 Private key (Bob) de335ed0a378ad69c126171ca7d32d7cf165b78710c380464682e26221a2412f Public key (Alice) (8e000c13ddfca84395567b4069153dbfb8c429ee952a2bddcc7a23a57e4d55bc,3cc7454f085fa6d69263d6f85685c355ebebc4191b4f57a162c9dfc72d9f8760) Public key (Bob) (88349ac178ee8af8aa4d2f303d677a3a44e48354a48d44873b7ca02cac116f6f 9f593df72e2c2b6fc3a059a40af4076202f02827ad1c04a4367a7b0ee41c776a) Shared key (Alice) 28bdb8e4bb311ea3e09893a1d3a6fc0db9094fa21b8597af57cb57addbfa1d98 Shared key (Bob) 28bdb8e4bb311ea3e09893a1d3a6fc0db9094fa21b8597af57cb57addbfa1d98
Theory
The following is a presentation on elliptic curves:
Overall an elliptic curve has the form of \(y^2 = x^3 + ax + b\), and where a and b are one of the defined parameters. Within Elliptic Curve Cryptography (ECC), we pick a point on the curve (\(G\) - the generator), and perform our operations with the modulus of \(p\). The final parameter are \(n\) - the size of a subgroup - and \(h\) - the cofactor. There are many different elliptic curve standards, including secp256k1, p192, p224, p256, and p384. The parameters are typically defined as \((p,a,b,G,n,h)\).
For secp256k1 (as used in Bitcoin) we use the parameters of:
- p=0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
- a=0
- b=7
- g= (0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
- n=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
- h=1
This gives an elliptic curve of:
\(y^2 = x^3+7\)
with a prime number (p) of 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
and which is \( 2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1 \)
All our operations will be (mod p)
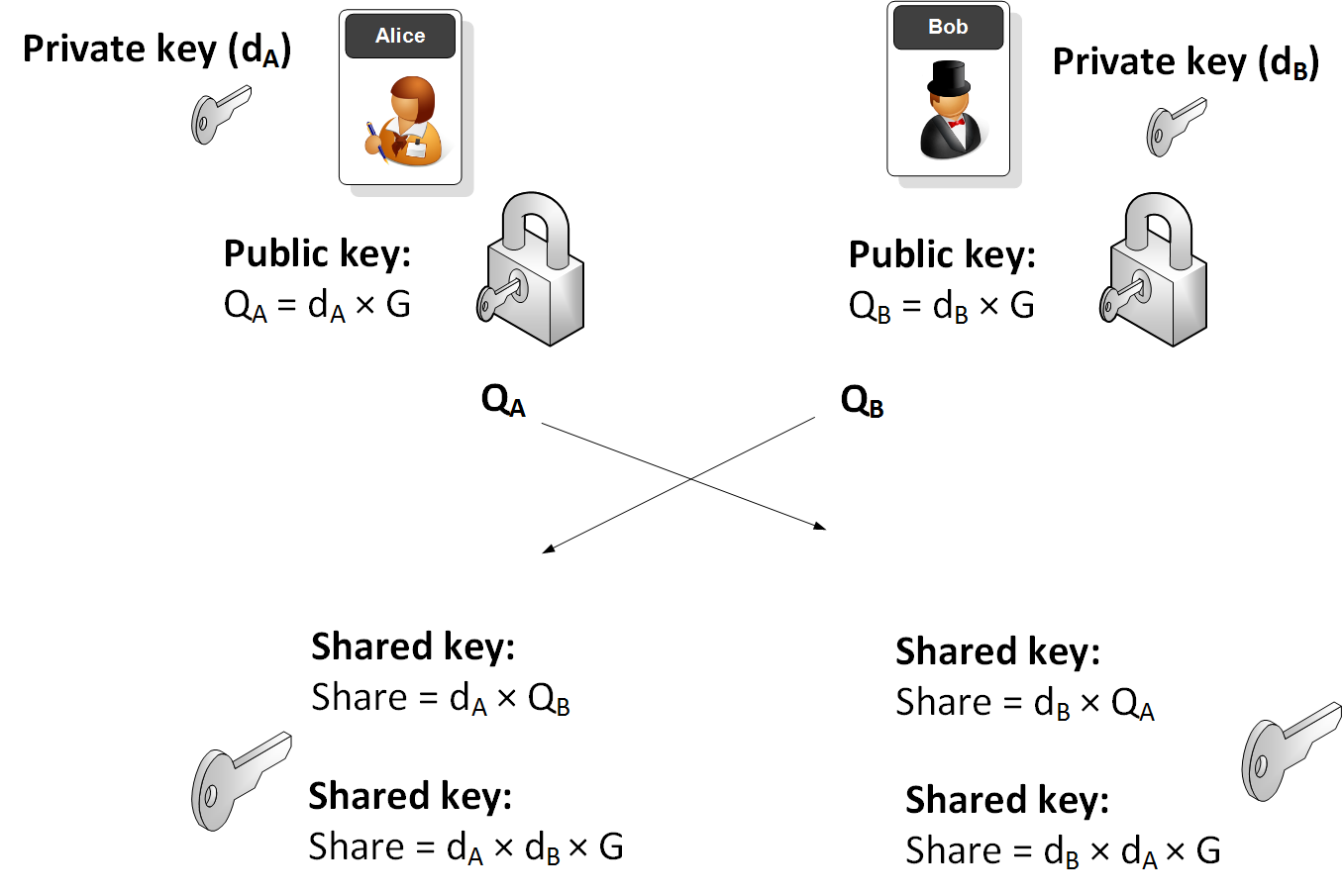
Elliptic Curve Diffie Hellman (ECDH)
ECDH is used to create a shared key. Bob will generate a public key and a private key by taking a point on the curve. The private key is a random number (\(d_B\)) and the Bob's public key (\(Q_B\)) will be:
\(Q_B = d_B \times G\)
Alice will do the same and generate her public key (\(Q_A\)) from her private key (\(d_A\)):
\(Q_A = d_A \times G\)
They then exchange their public keys. Alice will then use Bob's public key and her private key to calculate:
SharekeyAlice\( = d_A \times Q_B\)
This will be the same as:
SharekeyAlice\( = d_A \times d_B \times G\)
Bob will then use Alice's public key and his private key to determine:
SharekeyBob \(= d_B \times Q_A\)
This will be the same as:
SharekeyBob\( = d_B \times d_A \times G\)
And the keys will thus match.
The following illustrates the process: