Homomorphic Cipher - 4-bit adder

Theory

The code uses the DGHV (Dijk, Gentry, Halevi and Vaikuntanathan) scheme [paper] and which is a fully homomorphic encryption scheme [1].

First we get a random number (p) and two random numbers (q and r), and then encrypt a single bit (m) with:

\(c = p \times q + 2 \times r +m \)

In this case p will be our secret key.

If 2r is smaller than p/2, we cipher with mod p we get:

\(d = (c \mod p) \mod 2\)

We have basically added noise to the value with the q and r values.

With this function we can add (OR) and multiply (AND).

In this example we create an encrypted 4-bit add function:

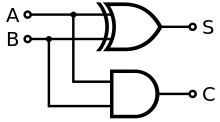
A half adder is created with:

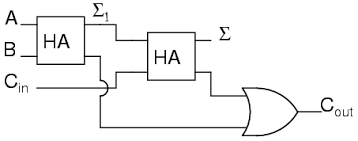
A full adder is created with:

For a Half-adder (HA), the logic is:

\(Sum=\bar{a}\cdot b + a \cdot \bar{b} \)

\(Carry=a + b \)

For a Full-adder (FA) we have inputs of a, b and \(C_{in}\), and which gives Sum and \(C_{out}\):

\(sum_1,c_1=HA(a,b)\)

\(Sum,c_2=HA(sum_1,cin)\)

\(C_{out}= c_1 + c_2\)

Code

The following is an outline and where I have used XOR, NOT, AND, HA and FA functions:

import sys
from random import randint

def tobits(val):
	l = [0]*(8)

	l[0]=val & 0x1
	l[1]=(val & 0x2)>>1
	l[2]=(val & 0x4)>>2
	l[3]=(val & 0x8)>>3
	return l

def XOR(a,b):
    return ( (NOT(a)*b) + (a*NOT(b)))

def NOT(val):
	return(val ^ 1)

def AND(a,b):
	return(a*b)

def OR(a,b):
	return(a+b)

def HA(bit1,bit2):
	sum=XOR(bit1,bit2)
	carryout=AND(bit1,bit2)
	return sum,carryout

def FA(bit1,bit2,cin):
	sum1,c1=HA(bit1,bit2)
	sum,c2=HA(sum1,cin)
	carryout=OR(c1,c2)
	return sum,carryout

def cipher(bit,p):
	q=randint(50000, 90000)	
	r=randint(1,200)
	return(  q * p + 2*r +int(bit)),q,r

val1=1
val2=1



if (len(sys.argv)>1):
       val1=int(sys.argv[1])
if (len(sys.argv)>2):
       val2=int(sys.argv[2])

v1=[]
v2=[]

v1=tobits(val1)
v2=tobits(val2)

cin=0

p =randint(3e23, 6e23)*2+1

c_carryin,q,r=cipher(cin,p)

print v1
print v2

cval1b0,q,r=cipher(v1[0],p)
cval2b0,q,r=cipher(v2[0],p)

cval1b1,q,r=cipher(v1[1],p)
cval2b1,q,r=cipher(v2[1],p)

cval1b2,q,r=cipher(v1[2],p)
cval2b2,q,r=cipher(v2[2],p)

cval1b3,q,r=cipher(v1[3],p)
cval2b3,q,r=cipher(v2[3],p)


print "1 ",c_carryin
c_sum1,c_carryout=FA(cval1b0,cval2b0,c_carryin )
c_sum2,c_carryout=FA(cval1b1,cval2b1,c_carryout )
c_sum3,c_carryout=FA(cval1b2,cval2b2,c_carryout )
c_sum4,c_carryout=FA(cval1b3,cval2b3,c_carryout )

#decrypt

sum1 = (c_sum1 % p) % 2
sum2 = (c_sum2 % p) % 2
sum3 = (c_sum3 % p) % 2
sum4 = (c_sum4 % p) % 2

carryout = (c_carryout % p) % 2

print "Val1:",val1
print "Val2:",val2

print "\nResults"

print "Sum:\t\t",carryout,sum4,sum3,sum2,sum1

A sample run for 10+3 is:

====Results
Sum:		0 1 1 0 1


=====Values
Val1:	10
Val2:	3
Val1:	[0, 1, 0, 1, 0, 0, 0, 0]
Val1:	[1, 1, 0, 0, 0, 0, 0, 0]
==============
CipherSum1:
1853413439219588680362570004035539833199755116203941462387881614051069375577231539520832
CipherSum2:
18432088486623813969980647304350337154711815732175283443172417318749729314891009826471766488723050656491638014592763859568974471673016023927866810
CipherSum3:
350105144711158283115794663725335113049840194441122465890305291670175445319366318657618638280532769541121410516476447411821501389646124250137985987070461181752715150777041165828342101068104481973550579462
CipherSum4:
3995391850663852786441324241749498886121148237476111383649056346858553730949171138764761675781807650455657359442677684602690077760551518453319562392807728988377765423915052651245069195389895502097424541686398830447980094072881739759138034496479585192950087562392

Presentation

Here is a presentation on the method used:

Reference

[1] M. van Dijk, C. Gentry, S. Halevi and V. Vaikuntanathan, "Fully
  Homomorphic Encryption over the Integers". Proceedings of Eurocrypt
  2010.