This is a simple abstraction of homomorphic cipher for 2-bit Adder. In this case we are adding a and b, and where a is defined with \(a_1 a_0\) and b is \(b_1 b_0\):
Simple Homomorphic Cipher for 2-bit Adder |
Theory
The code uses the DGHV (Dijk, Gentry, Halevi and Vaikuntanathan) scheme [paper] and which is a fully homomorphic encryption scheme [1].
First we get a random number (p) and two random numbers (q and r), and then encrypt a single bit (m) with:
\(c = p \times q + 2 \times r +m \)
In this case p will be our secret key.
If 2r is smaller than p/2, we cipher with mod p we get:
\(d = (c \mod p) \mod 2\)
We have basically added noise to the value with the q and r values.
With this function we can add (XOR) and multiply (AND).
In this example we create an encrypted 2-bit adder function (but which can easily be expanded to adding and multiplying values. The basic schematic is:
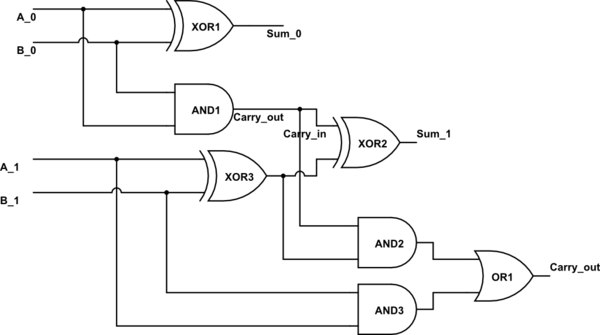
The logic is then:
\(Z_0=a_0 \oplus b_0\)
\(Z_0 (carry) =a_0 \cdot b_0\)
\(Z_1=a_1 \oplus b_1 \oplus Z_0 (carry)\)
\(Z_1 (carry) = (a_1 \cdot b_1) \oplus (a_1 \cdot Z_0 (carry)) \oplus (b_1 \cdot Z_0 (carry)) \)
Code
The following is an outline:
import sys
from random import randint
bit_a0 = 0
bit_a1 = 0
bit_b0 = 0
bit_b1 = 0
r1 =randint(1, 10)
r2= randint(1, 10)
r3 =randint(1, 10)
r4 =randint(1, 10)
q1 =randint(10000, 20000)
q2 =randint(10000, 20000)
q3 =randint(10000, 20000)
q4 =randint(10000, 20000)
p =randint(10000, 20000)
c_bit_a0 = q1 * p + 2*r1 +bit_a0
c_bit_a1 = q2 * p + 2*r2 +bit_a1
c_bit_b0 = q3 * p + 2*r3 +bit_b0
c_bit_b1 = q4 * p + 2*r4 +bit_b1
# 2-bit full adder
z0_add = (c_bit_a0 + c_bit_b0)
z0_carry = (c_bit_a0 * c_bit_b0)
z1_add = (c_bit_a1 + c_bit_b1 + z0_carry)
z1_carry = (c_bit_a1 * c_bit_b1) + (c_bit_a1 * z0_carry) + (c_bit_b1 * z0_carry)
print("r values:\t",r1,r2,r3,r4)
print("q values:\t",q1,q2,q3,q4)
print("p value:\t",p)
print("\nEncrypted bits")
print("---------------")
print("a0\t\t",c_bit_a0)
print("a1\t\t",c_bit_a1)
print("b0\t\t",c_bit_b0)
print("b1\t\t",c_bit_b1)
print("\nEncrypted values")
print("---------------")
print("Z0_add\t\t",z0_add)
print("Z0_carry\t",z0_carry)
print("Z1_add\t\t",z1_add)
print("Z1_carry\t",z1_carry)
#decrypt
z0 = (z0_add % p) % 2
z1 = (z1_add % p) % 2
z2 = (z1_carry % p) % 2
print("\nResults")
print(' ',bit_a1,bit_a0)
print('+', end=' ')
print(bit_b1,bit_b0)
print('-------')
print(z2,z1,z0)
Presentation
Here is a presentation on the method used:
Reference
[1] M. van Dijk, C. Gentry, S. Halevi and V. Vaikuntanathan, "Fully Homomorphic Encryption over the Integers". Proceedings of Eurocrypt 2010.