Simple Homomorphic Cipher for checking if Bob older

[Back] This is a simple abstraction of homomorphic cipher for a decision if Bob is older than Alice. In this case we will define Bob and Alice's age will be defined in two bit binary values: 00 (0 - 10 years), 01 (10 - 20 years), 10 (20 - 30 years), and 11 (over 30 years):

Theory

The code uses the DGHV (Dijk, Gentry, Halevi and Vaikuntanathan) scheme [paper] and which is a fully homomorphic encryption scheme [1].

First we get a random number (p) and two random numbers (q and r), and then encrypt a single bit (m) with:

\(c = p \times q + 2 \times r +m \)

In this case p will be our secret key.

If 2r is smaller than p/2, we cipher with mod p we get:

\(d = (c \mod p) \mod 2\)

We have basically added noise to the value with the q and r values.

With this function we can add (XOR) and multiply (AND).

In this example we will create a True Table for Bob (\(b_0b_1\) and Alice (\(a_1a_0\)). In this case we will return a 1 if Bob is older, and a 0 is he is not:

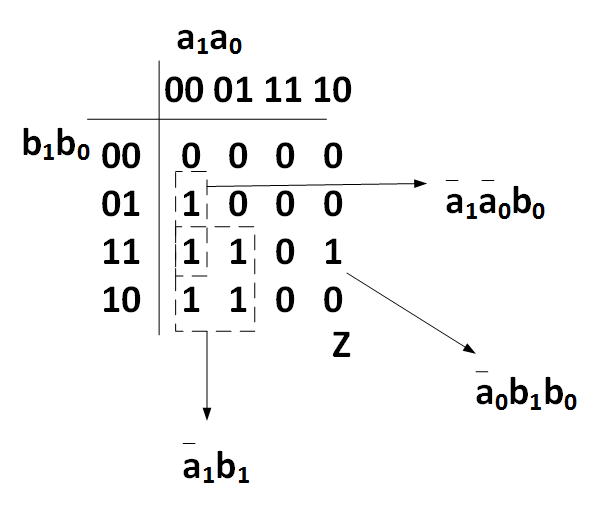
The logic is then:

\(Z_0=\bar{a_1} {b_1} + \bar{a_1} \bar{a_0} b_0 + \bar{a_0} b_1 b_0\)

Code

The following is an outline:

import sys
from random import randint

a_0 = 0
a_1 = 0
b_0 = 1
b_1 = 0

def inv(val):
	return(val ^ 1)
	
r1 =randint(1, 5)
r2= randint(1, 5)
r3 =randint(1, 5)
r4 =randint(1, 5)

q1 =randint(50000, 60000)
q2 =randint(50000, 60000)
q3 =randint(50000, 60000)
q4 =randint(50000, 60000)


p =randint(10000, 20000)


c_bit_a_0 =  q1 * p + 2*r1 +a_0
c_bit_a_1 =  q2 * p + 2*r2 +a_1 
c_bit_b_0 =  q3 * p + 2*r3 +b_0 
c_bit_b_1=  q4 * p + 2*r4 +b_1

# Truth table

cipher_older = inv(c_bit_a_1)*c_bit_b_1 + inv(c_bit_a_1)*inv(c_bit_a_0)*c_bit_b_0  + inv(c_bit_a_0)*c_bit_b_1*c_bit_b_0


			
print("r values:\t",r1,r2,r3,r4)
print("q values:\t",q1,q2,q3,q4)
print("p value:\t",p)

print("\nInput bits")
print("---------------")
print("a_1:\t",a_1, "a_0:\t",a_0)
print("b_1:\t",b_1, "b_0:\t",b_0)

print("\nCipherbits")
print("---------------")
print("a:\t",c_bit_a_0, "b:\t",c_bit_a_1)
print("c:\t",c_bit_b_1, "d:\t",c_bit_b_1)

print("\nCipher result")
print("---------------")
print("Result:\t",cipher_older)

#decrypt
result = (cipher_older % p) % 2

print("\nResults")
print(result)
if (result==1):
	print("Bob is older than Alice")
else:
	print("Bob is not older than Alice")

Presentation

Here is a presentation on the method used:

Reference

[1] M. van Dijk, C. Gentry, S. Halevi and V. Vaikuntanathan, "Fully
  Homomorphic Encryption over the Integers". Proceedings of Eurocrypt
  2010.

Simple Homomorphic Cipher for checking if Bob older

Parameters

Theory

Code

Presentation

Reference