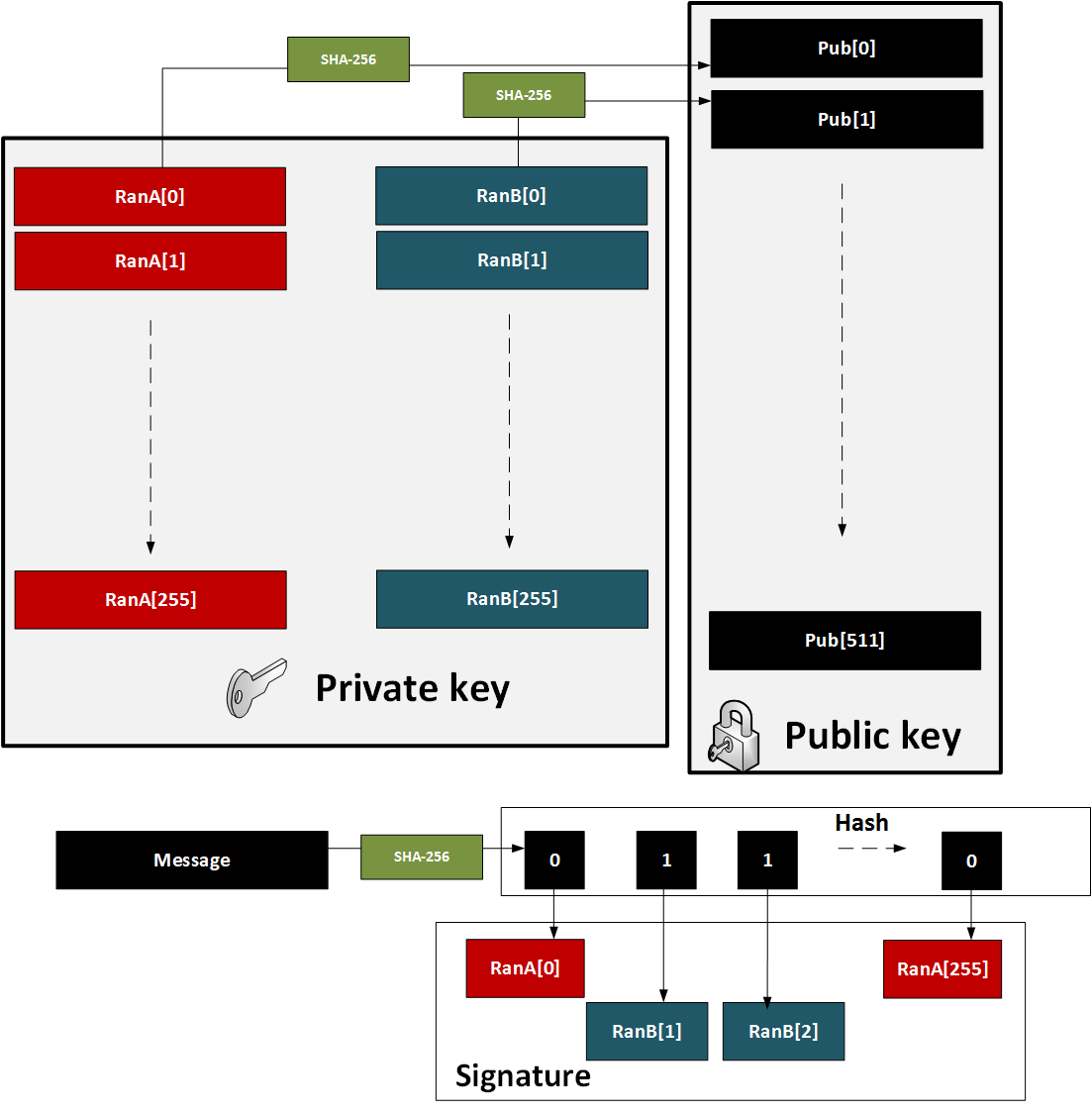
Sometime soon we perhaps need to wean ourselves of our existing public key methods, and look to techniques that are more challenging for quantum computers. With the implementation of Shor's alorigthm [here] on quantum computers, we will see our RSA and Elliptic Curve methods being replaced by methods which are quantum robust. One method is the Lamport signature method and which was created by Leslie B. Lamport in 1979 [1]. At the current time it is thought to be a quantum robust technique for signing messages. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
Quantum Robust: Lamport SignatureOutlineThe basic method of creating a Lamport hash signature is:
This process is illustrated below:
We can use the Lamport method for one-time signing, but, in its core format, we would need a new public key for each signing. The major problem with Lamport is thus that we can only sign once with each public key. We can overcome this, though, by creating a hash tree which is a merger of many public keys into single root. CodeAn outline of the code for the key generation is (based on code [here]):
import hmac
import hashlib
from binascii import unhexlify, hexlify
from math import ceil, floor, log
from os import urandom
import sys
message="Hello"
if (len(sys.argv)>1):
message=sys.argv[1]
def sha256(message):
return hashlib.sha256(message).hexdigest()
def sha256b(message):
return hashlib.sha256(message).digest()
def random_key(n=32): #returns a 256 bit hex encoded (64 bytes) random number
return hexlify(urandom(n))
def sign_lkey(priv, message): #perform lamport signature
signature = []
bin_lmsg = unhexlify(sha256(message))
print (bin_lmsg)
z = 0
for x in range (len(bin_lmsg)):
l_byte = bin(bin_lmsg[x])[2:] #[2:][-1:]
# l_byte = bin(ord(in_lmsg[x])[2:] #[2:][-1:]
while len(l_byte) < 8:
l_byte = '0'+ l_byte
for y in range(0,8):
if l_byte[-1:] == '0':
signature.append(priv[z][0])
l_byte = l_byte[:-1]
z+=1
else:
signature.append(priv[z][1])
l_byte = l_byte[:-1]
z+=1
return signature
def verify_lkey(signature, message, pub ): #verify lamport signature
bin_lmsg = unhexlify(sha256(message))
verify = []
z = 0
for x in range (len(bin_lmsg)):
l_byte = bin(bin_lmsg[x])[2:] #generate a binary string of 8 bits for each byte of 32/256.
# l_byte = bin(ord(bin_lmsg[x]))[2:]
while len(l_byte) < 8: #pad the zero's up to 8
l_byte = '0'+ l_byte
for y in range(0,8):
if l_byte[-1:] == '0':
verify.append((sha256(signature[z]),pub[z][0]))
l_byte = l_byte[:-1]
z+=1
else:
verify.append((sha256(signature[z]),pub[z][1]))
l_byte = l_byte[:-1]
z+=1
for p in range(len(verify)):
if verify[p][0] == verify[p][1]:
pass
else:
return False
return True
def random_lkey(numbers=256): #create random lamport signature scheme keypair
priv = []
pub = []
for x in range (numbers):
a,b = random_key(), random_key()
priv.append((a,b))
pub.append((sha256(a),sha256(b)))
return priv, pub
message = message.encode()
priv,pub = random_lkey()
print("==== Private key (keep secret) =====")
print("Priv[0][0] (SetA): ",priv[0][0])
print("Priv[0][1] (SetB): ",priv[0][1])
print("Priv[1][0] (SetA): ",priv[1][0])
print("Priv[1][1] (SetB): ",priv[1][1])
print("Priv[2][0] (SetA): ",priv[2][0])
print("Priv[2][1] (SetB): ",priv[2][1])
print("Priv[3][0] (SetA): ",priv[3][0])
print("Priv[3][1] (SetB): ",priv[3][1])
print("==== Public key (show everyone)=====")
print("Pub[0][0]: ",pub[0][0])
print("Pub[0][1]: ",pub[0][1])
print("Pub[1][0]: ",pub[1][0])
print("Pub[1][1]: ",pub[1][1])
print("==== Message to sign ===============")
print("Message:\t",message)
print("SHA-256:\t",sha256(message))
print("==== Signature =====================")
sign = sign_lkey(priv,message)
print("Sign[0]:\t",sign[0])
print("Sign[1]:\t",sign[1])
print("Sign[2]:\t",sign[2])
print("Sign[3]:\t",sign[3])
print("The signature test is ",verify_lkey(sign,message,pub))
A sample run which just shows the first few private key and the first public keys: ==== Private key (keep secret) ===== Priv[0][0] (SetA): 6f74f11f20953dc91af94e15b7df9ae00ef0ab55eb08900db03ebdf06d59556c Priv[0][1] (SetB): 4b1012fc5669b45672e4ab4b659a6202dd56646371a258429ccc91cdbcf09619 Priv[1][0] (SetA): 19f0f71e913ca999a23e152edfe2ca3a94f9869ba973651a4b2cea3915e36721 Priv[1][1] (SetB): 04b05e62cc5201cafc2db9577570bf7d28c77e923610ad74a1377d64a993097e Priv[2][0] (SetA): 15ef65eda3ee872f56c150a5eeecff8abd0457408357f2126d5d97b58fc3f24e Priv[2][1] (SetB): 8b5e7513075ce3fbea71fbec9b7a1d43d049af613aa79c6f89c7671ab8921073 Priv[3][0] (SetA): 1c408e62f4c44d73a2fff722e6d6115bc614439fff02e410b127c8beeaa94346 Priv[3][1] (SetB): e9dcbdd63d53a1cfc4c23ccd55ce008d5a71e31803ed05e78b174a0cbaf43887 ==== Public key (show everyone)===== Pub[0][0]: 7f2c9414db83444c586c83ceb29333c550bedfd760a4c9a22549d9b4f03e9ba9 Pub[0][1]: 4bc371f8b242fa479a20f5b6b15d36c2f07f7379f788ea36111ebfaa331190a3 Pub[1][0]: 663cda4de0bf16a4650d651fc9cb7680039838d0ccb59c4300411db06d2e4c20 Pub[1][1]: 1a853fde7387761b4ea22fed06fd5a1446c45b4be9a9d14f26e33d845dd9005f ==== Message to sign =============== Message: The quick brown fox jumps over the lazy dog SHA-256: d7a8fbb307d7809469ca9abcb0082e4f8d5651e46d3cdb762d02d0bf37c9e592 ==== Signature ===================== Sign[0]: 4b1012fc5669b45672e4ab4b659a6202dd56646371a258429ccc91cdbcf09619 Sign[1]: 04b05e62cc5201cafc2db9577570bf7d28c77e923610ad74a1377d64a993097e Sign[2]: 8b5e7513075ce3fbea71fbec9b7a1d43d049af613aa79c6f89c7671ab8921073 Sign[3]: 1c408e62f4c44d73a2fff722e6d6115bc614439fff02e410b127c8beeaa94346 The signature test is True In this case we take the random number, and then convert it to a string. So the SHA-256 signature of "6f74f11f20953dc91af94e15b7df9ae00ef0ab55eb08900db03ebdf06d59556c" is 7f2c9414db83444c586c83ceb29333c550bedfd760a4c9a22549d9b4f03e9ba9. If can be seen that the hash of message ("The quick brown fox jumps over the lazy dog") has a hex D value at the start, which is 1101 in binary, and we see we take from SetB [0], SetB [1], SetA [2] and SetB [3]. |
Reference
[1] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]