In many applications we need to generate a public key pair. With page produces a public key for SSH, PEM (an ASCII format) and DER (a bnary format):
SSH (Key gen) |
Background
So what are your company’s keys to the castle?
Well, for many, it is the SSH keys that support the accesses to cloud-based systems and code repositories. If these keys are compromised, it can lead to threats around the large scale loss of Intellectual Property (IP), data loss, and a whole lot of other things. Your company can also lose all digital trust in itself, and to external systems.
Most developers, for example, know that these key provide the core protection against a loss of their code, and where the management of these keys is now fundamental to the security of many organisations. For GitHub access, or for AWS and Azure accesses, it is magical public keys that give them trusted access. A loss of the private key associated with the public key, then, can mean a large scale breach of data, and a general loss of trust.
For an SSH connection, I’ll illustrate the process with Bob (the client) and Alice (the server):
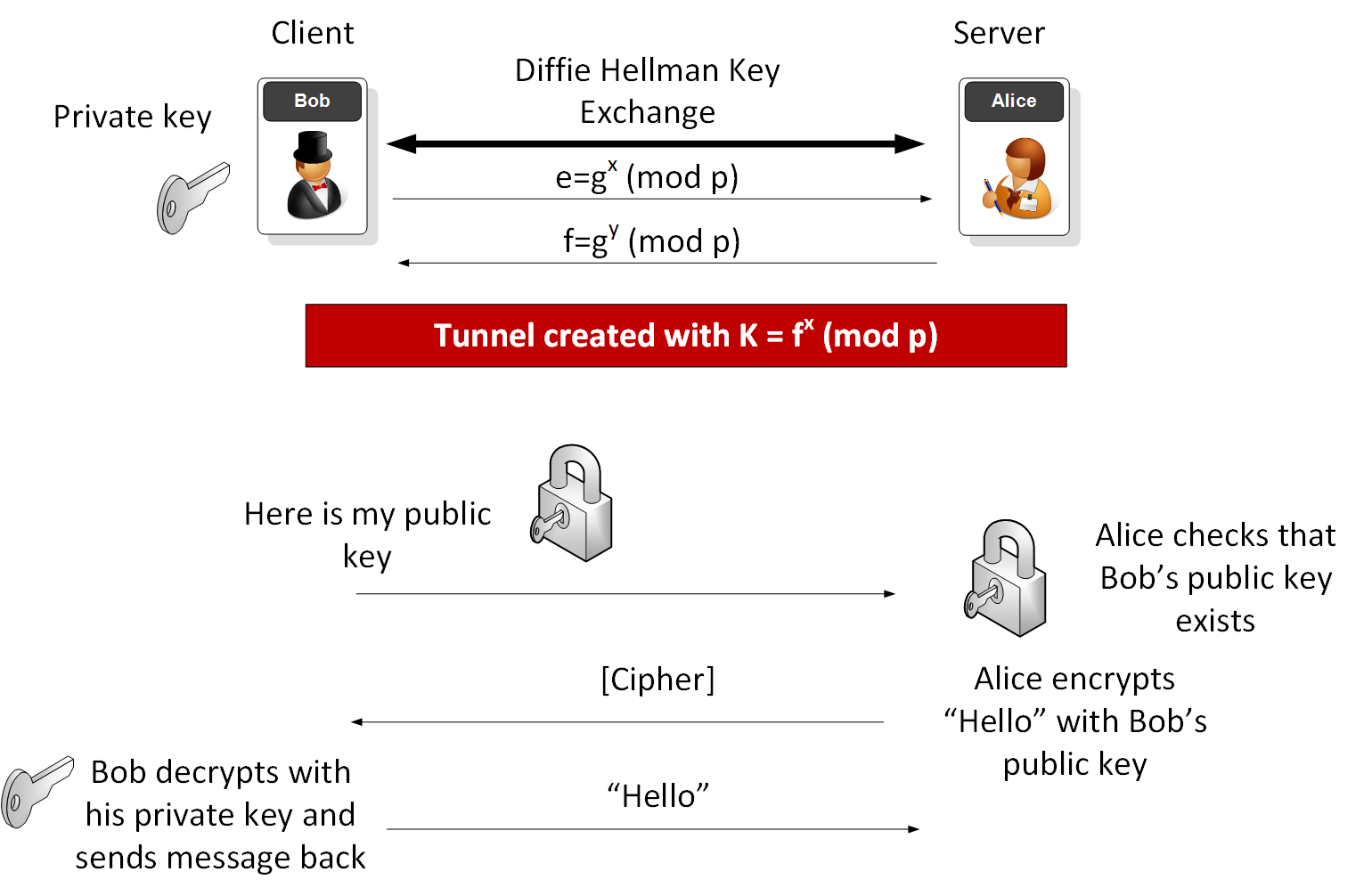
If Bob the Client is connecting to Alice the Server, he will generate a key pair (such as with RSA or Elliptic Curve methods), and put his public key file onto the server (normally this is stored with a .pub extension, and he will often copy and paste this into a file on the server). Alice then registers this as a valid key. Bob and/or Alice can revoke this key at any time. There are no risks to the public key being viewed by anyone.
Bob then connects to Alice and they might pick the Diffie-Hellman method of with a generator value (\(g\)) and the prime number (\(p\)). Bob then generates a random value (x) and passes \(e=g^x \pmod p\) to Alice. Alice then generates a random value (y) and passes \(f=g^y \pmod p\) to Bob. The shared key is then \(K= f^x \pmod p\) and which should be the same as \(e^y \pmod p\). Bob and Alice can now tunnel with the shared key, and using the symmetric key algorithm that they agreed on (such as ChaCha20, AES CTR or AES GCM).
No-one else will have the shared key (\(K\)) between Bob and Alice, even if they have been spying on their communications (as \(x\) and \(y\) are secret values).
Next — within the tunnel — Bob sends the public key that he wants to identify himself with, and Alice checks that it is registered. Alice then encrypts a message with Bob’s public key, and sends the encrypted message to him. As he is the only one with the required private key, he decrypts it, and sends the message back to Alice. Alice checks the message, and if it is the same as the one she encrypted, she knows she is talk with Bob, and so grants him access to the system.
So what does these magical keys actually look like? Well, on your Mac or our Linux machine, you have a special folder named .ssh and within it we store our keys. To generate an RSA key pair (a public key and a private key) we use:
ssh-keygen -t rsa -C "your email address"
The public key then becomes your identifier for secure connections. An example public key is:
ssh-rsa AAAAB3NzaC1yc2EAAAADAQABAAABAQDLrriuNYTyWuC1IW7H6yea3hMV+rm029m2f6IddtlImHrOXjNwYyt4Elkkc7AzOy899C3gpx0kJK45k/CLbPnrHvkLvtQ0AbzWEQpOKxI+tW06PcqJNmTB8ITRLqIFQ++ZanjHWMw2Odew/514y1dQ8dccCOuzeGhL2Lq9dtfhSxx+1cBLcyoSh/lQcs1HpXtpwU8JMxWJl409RQOVn3gOusp/P/0R8mz/RWkmsFsyDRLgQK+xtQxbpbodpnz5lIOPWn5LnT0si7eHmL3WikTyg+QLZ3D3m44NCeNb+bOJbfaQ2ZB+lv8C3OxylxSp2sxzPZMbrZWqGSLPjgDiFIBL fred@blogs
For elliptic curve we can use ECDSA:
ssh-keygen -t ecdsa -C "your email address"
The public key then has the format of:
ecdsa-sha2-nistp256 AAAAE2VjZHNhLXNoYTItbmlzdHAyNTYAAAAIbmlzdHAyNTYAAABBBE+y72Vqy52xgqo4aBJUZXKpqbsEpkiUvnCxtr+ZbPM3jyrr2ANl9Ivh66pa6fDwomAA+8SzgRlXV5QnVGQExoE= fred@blogs
and a private key of:
— — -BEGIN OPENSSH PRIVATE KEY — — - b3BlbnNzaC1rZXktdjEAAAAABG5vbmUAAAAEbm9uZQAAAAAAAAABAAAAaAAAABNlY2Rz... WVyLmFjLnVr -----END OPENSSH PRIVATE KEY-----
The public key is then ported onto the remote server, and will authenticate the client. Before we pass the public key, we must create an encrypted tunnel, so let’s look at the process for an SSH connection (and which normally uses TCP port 22 on the server to communicate with).
When we connect through ssh, we open up a communication channel where the server — with the Server: Key Exchange Init message— sends a range of algorithms that it would like to use for the key exchange, and also for the symmetric key algorithm. In the example given next, we see the key exchange methods include Curve29919 (Elliptic Curve) and Diffie-Hellman, and the symmetric key methods include ChaCha20/Poly1305, 192-bit AES (CTR) and 128-bit AES (GCM):
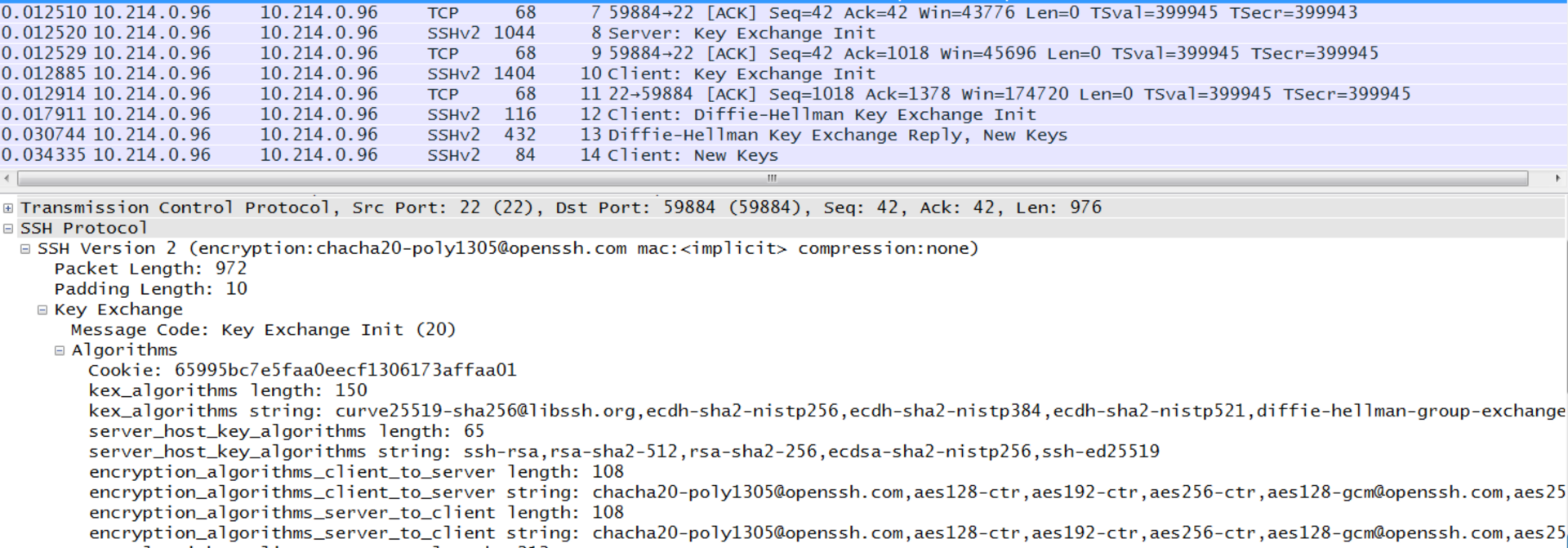
The client then does the same thing with a Client: Key Exchange Init message (SSH_MSG_KEXDH_INIT). The client and server then agree to the method used.
In the following example the client tells the server that it wants to use the Diffie-Hellman method to generate the session key, and sends its public value (e). For this the client generates a random value (x), and calculates a value of \(e\) (\(e=g^x \pmod p\)) and sends this to the server:
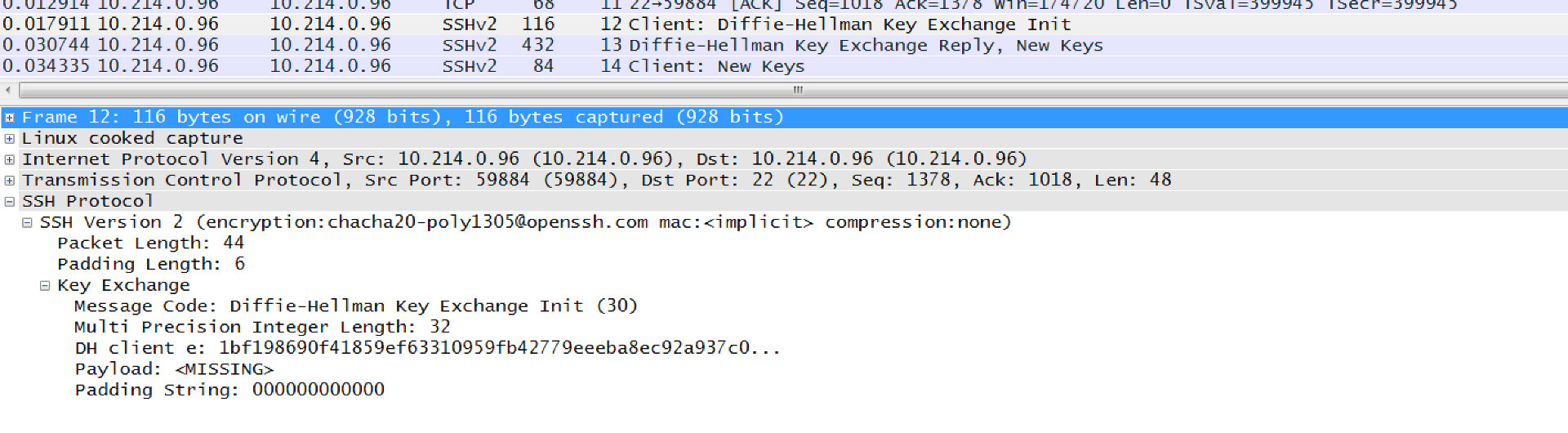
The server then generates a random value (y) and sends its public value (\(f=g^y \pmod p\)) as a Diffie-Hellman Key Exchange Reply, New Keys message (SSH_MSG_KEXDH_REPLY):
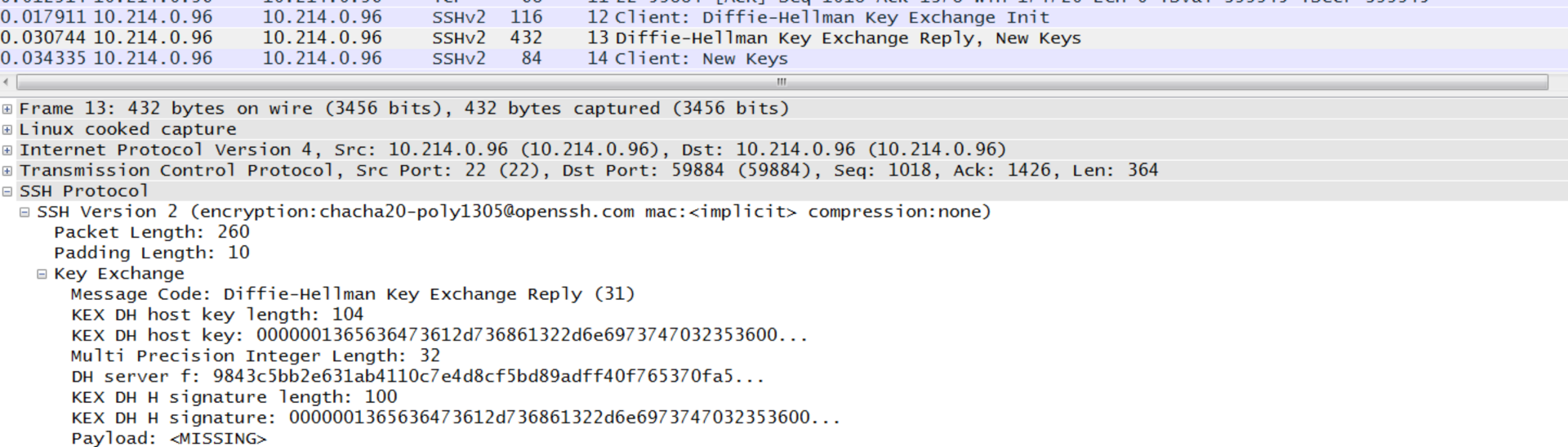
The client — which knows a secret of x — will receive f, and generate the shared key as:
\(K = f^x \pmod p\)
The server — which knows a secret of \(y\) — will generate the key as:
\(K = e^y \pmod p\)
The key exchange ends with a Client: New Keys (SSH_MSG_NEWKEYS) message:
Note the standard for diffie-hellman-group1-sha1 is to use Oakley Group 2, we have following values for \(p\) and \(g\):
The prime is 2^1024 - 2^960 - 1 + 2^64 * { [2^894 pi] + 129093 }.
FFFFFFFF FFFFFFFF C90FDAA2 2168C234 C4C6628B 80DC1CD1
29024E08 8A67CC74 020BBEA6 3B139B22 514A0879 8E3404DD
EF9519B3 CD3A431B 302B0A6D F25F1437 4FE1356D 6D51C245
E485B576 625E7EC6 F44C42E9 A637ED6B 0BFF5CB6 F406B7ED
EE386BFB 5A899FA5 AE9F2411 7C4B1FE6 49286651 ECE65381
FFFFFFFF FFFFFFFF
The generator (g) is 2
The values of g and p are thus well known to both the client and the server, and where there is no need to pass these. From the value of the prime number, we can see we are using a 1,024-bit value. In more secure environments, you should use Diffie Hellman Group 5 security and above. With Group 5 we have a 1,536-bit prime number and with Group 14 we have a 2,048 bit prime.
We can specify the hosts we trust and the methods used within the ./ssh/config file:
Host 8.8.8.8
KexAlgorithms +diffie-hellman-group1-sha1
Other options are:
diffie-hellman-group-exchange-sha1
diffie-hellman-group-exchange-sha256
diffie-hellman-group1-sha1
diffie-hellman-group14-sha1
ecdh-sha2-nistp256
ecdh-sha2-nistp384
ecdh-sha2-nistp521
We now should now have a shared key and the packets will now be encrypted with it. Next the client sends its public key to the server, and the server checks that it knows about it. The server then encrypts a message with the client’s public key, and send it to the client. The client must then decrypt this message with its private key and then send it back, for the server to check. If correct, the server knows that the client is valid.
A sample run gives:
Generate public key (1,204 bits) Public key: ssh-rsa AAAAB3NzaC1yc2EAAAADAQABAAAAgQCwzh+C4XxgB0mce2+bB+rt9mF9nNBYtuCO82EHxACMWpsdz6vFjvM3StA0R44YFT2b5tHFa2+tbvMSHL0lYpPpIhNOUPkQ4DpTv+22ehpDN1/86yEF2UeG0PJIKpxLg9XQbybqNxSxWyrJDJshZvDu0WvWTtihE2twC2vbOKziHw== Private key (PEM) -----BEGIN RSA PRIVATE KEY----- MIICWwIBAAKBgQCwzh+C4XxgB0mce2+bB+rt9mF9nNBYtuCO82EHxACMWpsdz6vF jvM3StA0R44YFT2b5tHFa2+tbvMSHL0lYpPpIhNOUPkQ4DpTv+22ehpDN1/86yEF 2UeG0PJIKpxLg9XQbybqNxSxWyrJDJshZvDu0WvWTtihE2twC2vbOKziHwIDAQAB AoGAFZS7XO7oDxKkphCdEVfYkb5KrRn4hnOgGmLTu65tgLRIjc19AorN3jhoDJGV YxQopoB4p3fTNGDAE7xlTAxp0E2aLDuL/YNZY13ZIWxp318XAC3xLwLdNKxEoUoX F5ITS/dpwrLi/ActyNkhy94lFP8l7XVkwsUBSryLkjivg+kCQQDH5LeEWlwueWGy iXVcOlKPPOXCG4Sgd8E854YYmchkBF9bpFjFVBCkTPJ9ayd+Oe4civEJe5yH7p92 lDTBWNpnAkEA4m5oBXbgn0qs2z6cfzs7jwUEFsCztBu+THW5EhwPhxfDx1aHoYqk pTUbUXuhAmXnuLy2wwMecSXfpMDngIFXiQJAcqS/h/4XDmR5Xt8tWybsANDJaUlF CI+GWXrj0qooXwyO8E1SyGHNZZ3oGXxiWye4Y9BgK7MkdGWsOWMI2rcuEwJALHLh 5pi0dXCSSCOdUviMs4GXkOPZIvUDQT0mzGBHyAwpOXtJ+rMdqPSo3TD4pWDdwQ0C j3uQQUPfCBd6GmbJiQJAXtnZNWzuI7RjCPgZTZCmwDAJhIPJmCI9KLkSRR4vC3Lb IfTXKx6fr/3CZD0MhQ7jNL2ROOP3MqmCckSA6l9VBw== -----END RSA PRIVATE KEY----- Diffie Hellman Group 1 SHA1 key exchange Prime: 179769313486231590770839156793787452899496105780084477581364395941166029300994227248108142568843635979525217656468305187283113985859749391620117724605713213166583281361514260165573916676436384587380559654134976387464728712299852705313967066086226450531450329744102406706749410555665787151172640288690206146559 g: 2 Bob's random value (512-bit): 12381421778935651834613565418485875449555163897934742376047213608162734104245041587708977954063043593389360807299555106385264576157482581773758110446880234 Alice's random value (512-bit): 1489805871059747417954470368838655324839313539141183558629503207401483755764971847254527959331402155513413039000732445217698577463403887489988542053942880 Shared key: 120108935013672105663120250420884162159451869199425857627692298338457470156854927571467077588460550431387293141168682258069614461504680375958559252485100174597947741731931065201722474145979130943004552512711143147537889465065324245747427471825543577674644504472526410769982889024918673035441434433368963121185
The Wireshark trace is [here] and the source code for SSH is [here].
Coding
The outline of the code is:
import os
import sys
import random
from Crypto.PublicKey import RSA
import math
type='OpenSSH'
print('Generate public key (1,204 bits)')
print()
key = RSA.generate(1024, os.urandom)
pubkey = key.publickey()
print()
print("Public key: \n",pubkey.exportKey(type))
print("\nPrivate key (PEM)")
print(key.exportKey('PEM'))
if (type=='OpenSSH'):
p=2**1024 - 2**960 - 1 + 2**64 * int(math.floor( 2**894 * math.pi + 129093 ))
g=2
print("\nDiffie Hellman Group 1 SHA1 key exchange")
print("Prime: ",p)
print("g: ",g)
x = random.getrandbits(512)
y = random.getrandbits(512)
print("Bob's random value (512-bit):",x)
print("Alice's random value (512-bit):",y)
e = pow(g, x, p)
K= pow(g,y,p)
print("Shared key:",K)
Presentation
The following is a presentation [Slides]: