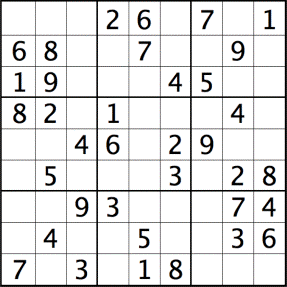
Suduko solver with Z3The Z3 library was developed by Microsoft Research and can be used as a prover/solver. In this case we use Z3 to solve a suduko puzzle: ExampleIn this case we start with:
and the answer is:
CodingThe following example is taken from the Z3 Web site [here]:
from z3 import *
# 9x9 matrix of integer variables
X = [ [ Int("x_%s_%s" % (i+1, j+1)) for j in range(9) ] for i in range(9) ]
# each cell contains a value in {1, ..., 9}
cells_c = [ And(1 <= X[i][j], X[i][j] <= 9) for i in range(9) for j in range(9) ]
# each row contains a digit at most once
rows_c = [ Distinct(X[i]) for i in range(9) ]
# each column contains a digit at most once
cols_c = [ Distinct([ X[i][j] for i in range(9) ]) for j in range(9) ]
# each 3x3 square contains a digit at most once
sq_c = [ Distinct([ X[3*i0 + i][3*j0 + j] for i in range(3) for j in range(3) ])
for i0 in range(3) for j0 in range(3) ]
sudoku_c = cells_c + rows_c + cols_c + sq_c
# sudoku instance, we use '0' for empty cells
instance = ((0,0,0,2,6,0,7,0,1),
(6,8,0,0,7,0,0,9,0),
(1,9,0,0,0,4,5,0,0),
(8,2,0,1,0,0,0,4,0),
(0,0,4,6,0,2,9,0,0),
(0,5,0,0,0,3,0,2,8),
(0,0,9,3,0,0,0,7,4),
(0,4,0,0,5,0,0,3,6),
(7,0,3,0,1,8,0,0,0))
if (len(sys.argv)>1):
instance=eval("("+sys.argv[1]+")")
print ("The solution is:")
instance_c = [ If(instance[i][j] == 0,
True,
X[i][j] == instance[i][j])
for i in range(9) for j in range(9) ]
s = Solver()
s.add(sudoku_c + instance_c)
if s.check() == sat:
m = s.model()
r = [ [ m.evaluate(X[i][j]) for j in range(9) ]
for i in range(9) ]
print_matrix(r)
else:
print ("failed to solve")
|