We can implement a scheme with oblivious transfer and ZPK using a blinding factor within elliptic curve methods.
EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function) |
Method
So how can Bob purchase 10 vouchers for presents for Carol, Trent and Faith, and then for Alice’s store to not be able to tell it was Bob who had bought them. For this, we can turn to obvious transfer, and zero-knowledge proof (ZPK) method. One of the best around uses the power of elliptic curve methods and is defined as EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function).
Now Bob wants to buy 10 vouchers from Alice, and he wants to give them to Carol, Trent and Faith. For this he generates 10 random numbers (\(x_1\), \(x_2\), … \(x_{10}\)). He then matches these onto elliptic curve points (finding the nearest x-axis point). For these 10 vouchers, he then creates a random value for a blinding factor (\(b\)). Bob then multiplies each of the elliptic curve points with \(b\), and hands these 10 elliptic curve points to Alice, and pays for 10 vouchers.
Alice then multiplies each of these points with her private key (\(k\)), and sends them back to Bob. When Bob receives these he now unblinds each voucher by dividing each of them by his blinding factor (\(b\)). The values he now has are \(k \times X_1\), \(k \times X_2\), … \(k \times X_{10}\).
Next, Bob gives Carol the values of \(X_1\) and \(k \times X_1\), \(X_2\) and \(k \times X_2\) to Trent, and \(X_3\) and \(k \times X_3\) to Faith. Each of them can then go to Alice’s shop and give Alice their values. For Carol, Alice then checks that the value of X1 multiplied by her private key (\(k\)) is the other value that Carol has given her (\(k \times X_1\)). If this checks out, she will approve the purchase, but will not know where the voucher came from. For this only Bob is able to generate the values of \(X_1\) and \(k \times X_1\), as Alice only knows \(k\).
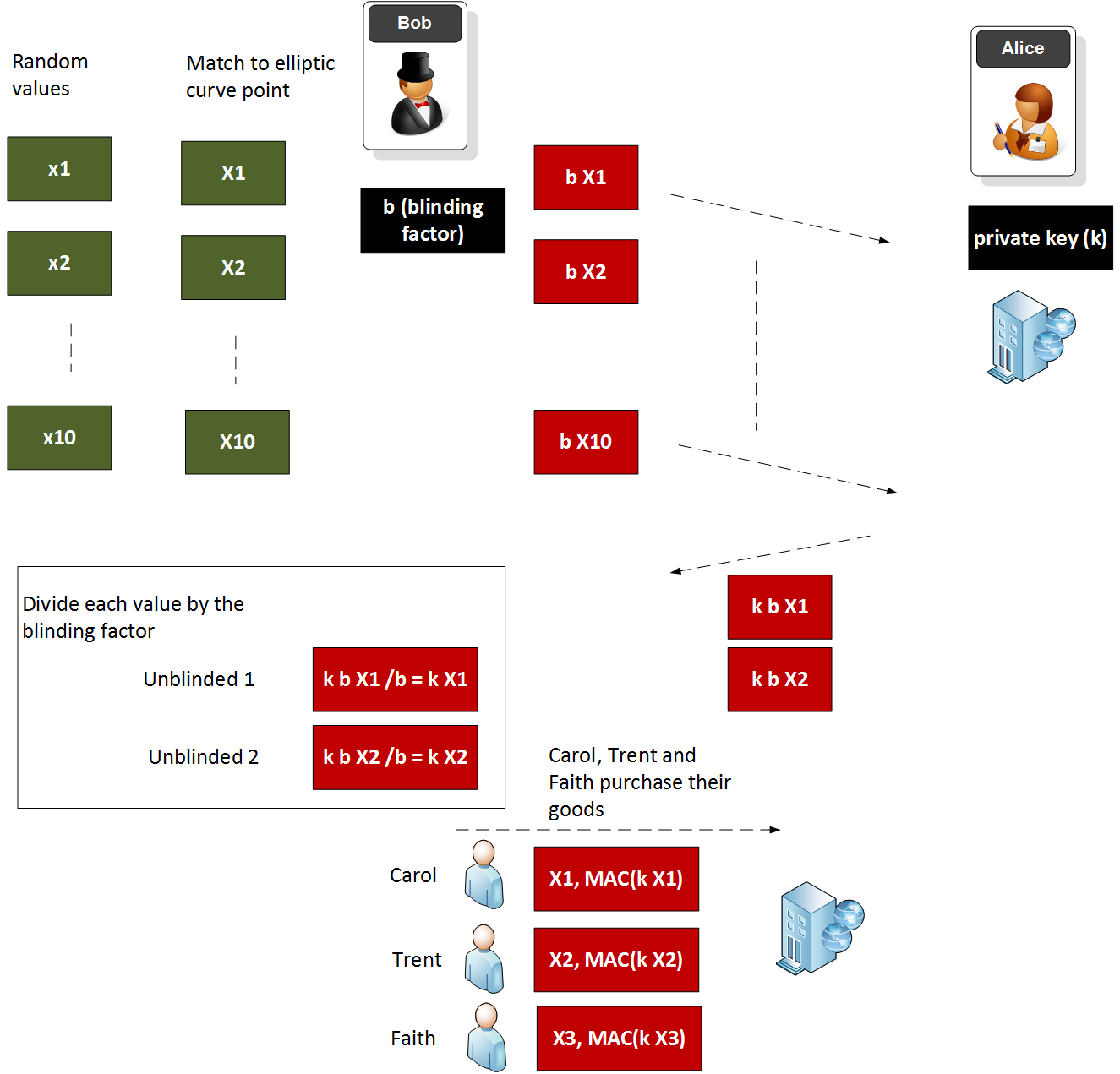
And there you go. We have created a world where Alice cannot determine where the vouchers came from, and we have preserved the rights of Bob to privacy. We have also created purchase receipts which can be trusted, but which cannot be tracked. If an auditor wants to resolve, Bob can reveal his blinding factor.
A sample run with a blinding factor of 200 is:
Bob's secret key: 14740736474426194531991971984653537731905408749855764823599798340081744951236 Bob's public key: (93337810080056808509143628030711186374649707518966393007145508355141043725976L, 89984156688937262044671618721504988493956786224984493903982837891549653699065L) Alice's private key: 89305535952581699375152380663798359425217323217249314939419531091958137015823 Bob's blinding value: 200 ========================== Bob sends: (18596347454806314617546420688351915830023283853668514133074243099405745649845L, 64617527428093632813388283524274192193044853232912157518001869558548410052218L) Alice sends: (31878088913995653806919695713432488276334299481378560104342584683002673166698L, 103705587118533077091760072597215457686031621435501948801185592847662523540405L) Divide by blinding: (17518998733162042340917617062932188545103969459451983686440483965055076635903L, 110235880626729109887528707294137377769315565282992016601256532683996902787041L) Alice Private Key times Bob Public: (17518998733162042340917617062932188545103969459451983686440483965055076635903L, 110235880626729109887528707294137377769315565282992016601256532683996902787041L)
Coding
The following is an outline of the code:
import collections
import hashlib
import random
import binascii
import sys
EllipticCurve = collections.namedtuple('EllipticCurve', 'name p a b g n h')
curve = EllipticCurve(
'secp256k1',
# Field characteristic.
p=0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f,
# Curve coefficients.
a=0,
b=7,
# Base point.
g=(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798,
0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8),
# Subgroup order.
n=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141,
# Subgroup cofactor.
h=1,
)
# Modular arithmetic ##########################################################
def inverse_mod(k, p):
"""Returns the inverse of k modulo p.
This function returns the only integer x such that (x * k) % p == 1.
k must be non-zero and p must be a prime.
"""
if k == 0:
raise ZeroDivisionError('division by zero')
if k < 0:
# k ** -1 = p - (-k) ** -1 (mod p)
return p - inverse_mod(-k, p)
# Extended Euclidean algorithm.
s, old_s = 0, 1
t, old_t = 1, 0
r, old_r = p, k
while r != 0:
quotient = old_r // r
old_r, r = r, old_r - quotient * r
old_s, s = s, old_s - quotient * s
old_t, t = t, old_t - quotient * t
gcd, x, y = old_r, old_s, old_t
assert gcd == 1
assert (k * x) % p == 1
return x % p
# Functions that work on curve points #########################################
def is_on_curve(point):
"""Returns True if the given point lies on the elliptic curve."""
if point is None:
# None represents the point at infinity.
return True
x, y = point
return (y * y - x * x * x - curve.a * x - curve.b) % curve.p == 0
def point_add(point1, point2):
"""Returns the result of point1 + point2 according to the group law."""
assert is_on_curve(point1)
assert is_on_curve(point2)
if point1 is None:
# 0 + point2 = point2
return point2
if point2 is None:
# point1 + 0 = point1
return point1
x1, y1 = point1
x2, y2 = point2
if x1 == x2 and y1 != y2:
# point1 + (-point1) = 0
return None
if x1 == x2:
# This is the case point1 == point2.
m = (3 * x1 * x1 + curve.a) * inverse_mod(2 * y1, curve.p)
else:
# This is the case point1 != point2.
m = (y1 - y2) * inverse_mod(x1 - x2, curve.p)
x3 = m * m - x1 - x2
y3 = y1 + m * (x3 - x1)
result = (x3 % curve.p,
-y3 % curve.p)
assert is_on_curve(result)
return result
def scalar_mult(k, point):
"""Returns k * point computed using the double and point_add algorithm."""
assert is_on_curve(point)
if k % curve.n == 0 or point is None:
return None
if k < 0:
# k * point = -k * (-point)
return scalar_mult(-k, point_neg(point))
result = None
addend = point
while k:
if k & 1:
# Add.
result = point_add(result, addend)
# Double.
addend = point_add(addend, addend)
k >>= 1
assert is_on_curve(result)
return result
# Keypair generation ################################################
def make_keypair():
"""Generates a random private-public key pair."""
private_key = random.randrange(1, curve.n)
public_key = scalar_mult(private_key, curve.g)
return private_key, public_key
b=13
if (len(sys.argv)>1):
b=int(sys.argv[1])
bobSecretKey, bobPublicKey = make_keypair()
aliceSecretKey, alicePublicKey = make_keypair()
print("\nBob\'s secret key:\t", bobSecretKey)
print("Bob\'s public key:\t", bobPublicKey)
print("Alice\'s private key:\t", aliceSecretKey)
print("Bob's blinding value:\t",b)
print("==========================")
bobsend = scalar_mult(b,bobPublicKey)
print ("Bob sends:\t",bobsend)
alicesend = scalar_mult(aliceSecretKey,bobsend)
print ("Alice sends:\t",alicesend)
val = scalar_mult(inverse_mod(b,curve.n),alicesend)
print ("Divide by blinding:\t",val)
val2 = scalar_mult(aliceSecretKey,bobPublicKey)
print ("Alice Private Key times Bob Public:\t",val2)
x1,y1=val
x2,y2=val2
if (x1==x2): print ("They match!!!")
And outline is here [sldies]:
For voting [sldies]: