With Feige-Fiat-Shamir zero-knowledge proof we can prove that we know something with actually revealing our information.
Feige-Fiat-Shamir zero-knowledge proof |
Outline
Why do we still pass our passwords over a network? Why do we still hash passwords? Why can’t we come up with our own random value, and then prove to everyone that we know the secret?
Well, the Feige-Fiat-Shamir method provides a zero-knowledge proof — created by Uriel Feige, Amos Fiat, and Adi Shamir in 1988 [paper] — and where Bob can prove something to Alice, without revealing the information that he has.
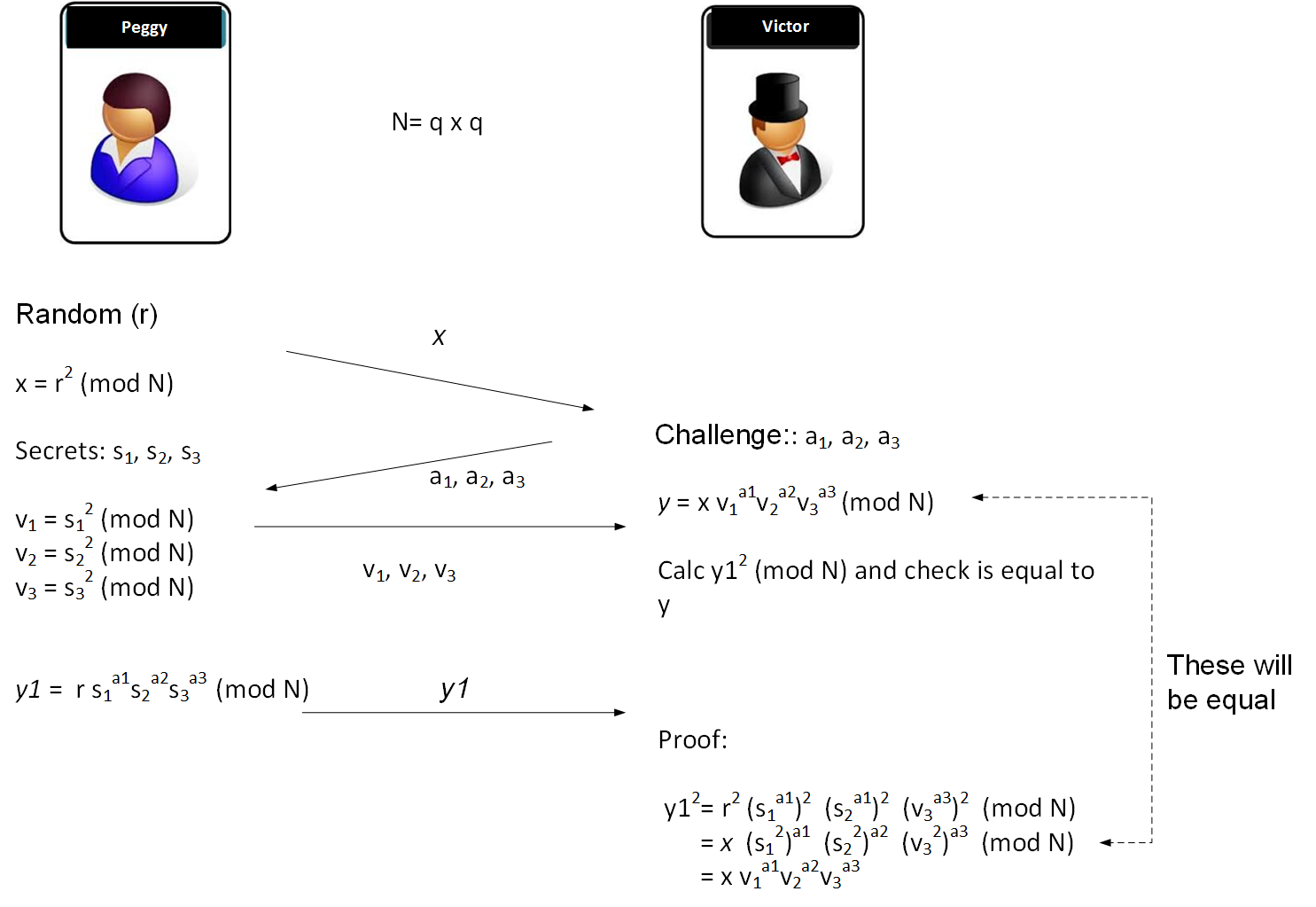
First Peggy (the prover) and Victor (the verifier) agree on two prime numbers (say 101 and 23), and calculate a value of \(N\) (101𝗑23), to give \(N\)=2,323.
Peggy has three secret numbers of \(s_1=5\); \(s_2=7\); and \(s_3=3\). Note that these numbers need to be co-prime to \(N\), so that they do not share a factor with \(N\). If we choose \(N\) as the multiplication of two prime numbers, we only need to avoid these numbers.
Now Victor generates three random numbers which are either 0 or a 1, such as \(a_1=1\); \(a_2=0\); and \(a_3=1\), and sends these to Peggy.
Next Peggy generates a random number (such as \(r=13\)). She then calculates a value of \(x\) which is:
\(x = (r^2) \pmod N\)
which gives \(x = 169\). Peggy sends this to Victor.
Peggy calculates:
\(y1 = r \times (s_1^{a_1}) \times (s_2^{a_2}) \times (s_3^{a_3}) \pmod N\)
This gives 195, which she sends to Victor.
Next Peggy then computes:
\(v_1=(s_1^2) \pmod N\)
\(v_2=(s_2^2) \pmod N\)
\(v_3=(s_3^2) \pmod N\)
She then sends these to Victor and who computes:
\( y = x \times (v_1^{a_1}) \times (v_2^{a_2}) \times (v_3^{a_3}) \pmod N\)
If \(y1^2 \pmod n\) is equal to \(y\) that Peggy has sent, then Peggy has proven that she knows the secret values.
Here is the code:
n=101*23
r=13
s1=5
s2=7
s3=3
a1=1
a2=0
a3=1
print ('N=',n)
x = (r**2) % n
print ('x=',x)
print ('s1=',s1,'s2=',s2,'s3=',s3)
print ('a1=',a1,'a2=',a2,'a3=',a3)
y = (r * ((s1**a1) * (s2**a2) * (s3**a3)) ) % n
print ('Y=',y, ' y^2 mod n = ',(y**2 % n))
v1=(s1**2) %n
v2=(s2**2) %n
v3=(s3**2) %n
y2 = (x * ( (v1**a1) * (v2**a2) * (v3**a3)) ) % n
print ('Y=',(y**2) %n)
and a sample run:
N= 2323
x= 169
s1= 5 s2= 7 s3= 3
a1= 1 a2= 0 a3= 1
Y= 195 y^2 mod n = 857
Y^2= 857
We can see the values are the same at the end. Alice can go through several rounds of providing a1, a2 … an, in order to prove that Bob knows the information.
Article
An article on the method is [here]