We can use the Fiat-Shamir heuristic with non-interactive random oracle access in order to prove that we know a secret. In this case the non-interactive oracle is a hash function [here]
Non-interactive random oracle access |
Method
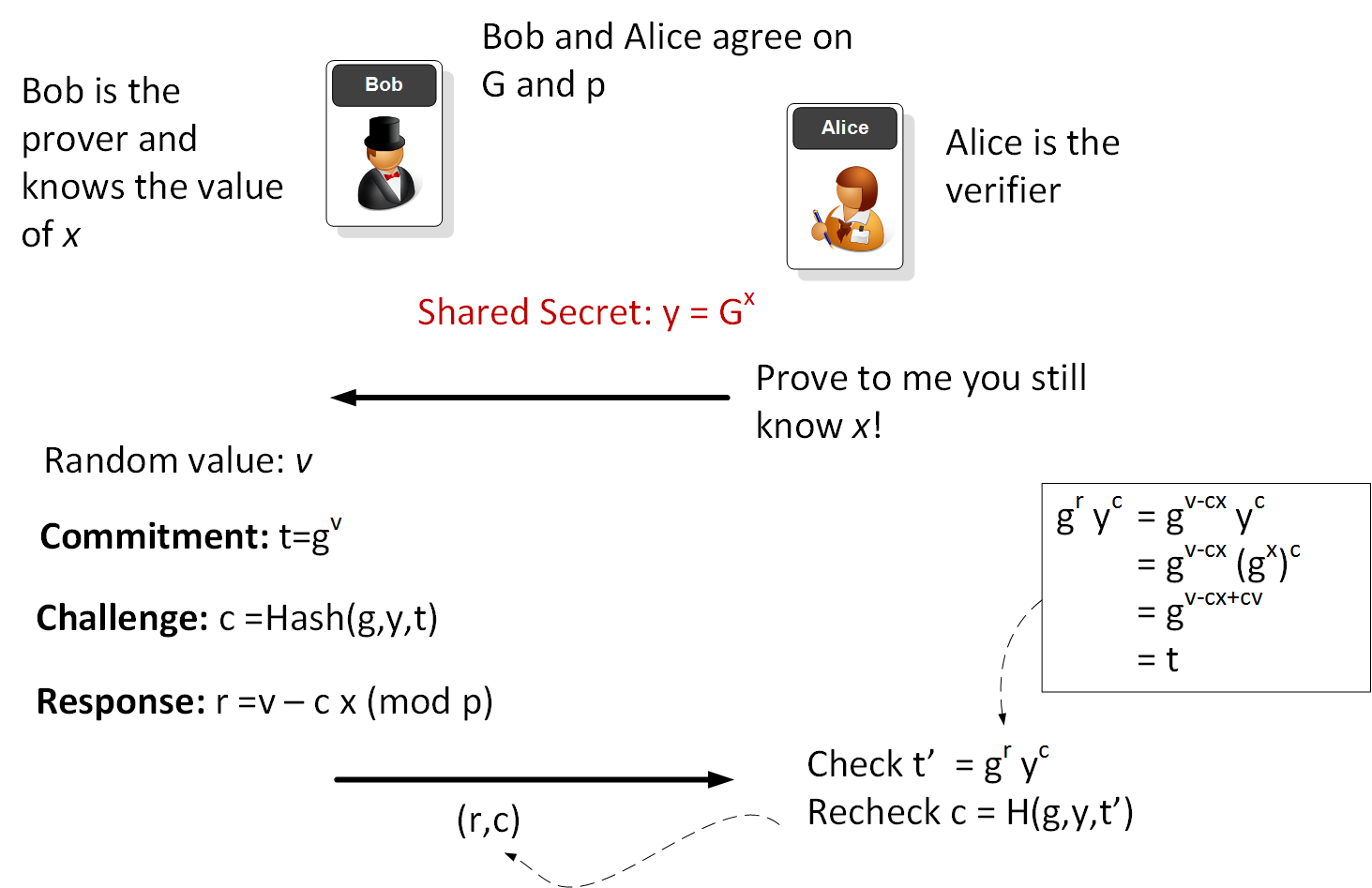
Alice can prove her identity with a little bit of a calculation, and then anyone who wants to prove her ID can then do a calculation, and if it is correct, she has proven herself. This is known as a "non-interactive random oracle access" for zero-knowledge proofs. In the case we will look at the use of a hash value for the non-interactive random oracle part.
Normally Alice would pass a random value to whoever it is that wants to prove her identity, but in this case she will use the hash value to randomise the puzzle and answer.
The stages are:
1. First everyone agrees on a puzzle and has a secret (x). The puzzle is:
\(y=g^x\)
where we agree on g and x is the secret that Alice proves that she knows. Let's say that g is 13, and x is 11, so \(g^x\) is:
1792160394037
2. Next Alice generates a random number (v) and calculates t, which is:
\(t = g^v\)
Let's say that the value of v is 8. This gives t of:
815730721
3. She now computes a hash value (c) created from g, y and t:
\(c = MD5(g+y+t)\)
Let's say this gives us 12 (we would normally limit the range of the value produced).
4. Now she computes r of \(r= v -c \times t\) to get:
-124
5. Now she sends out t and r to prove her identity:
[815730721, -124]
6. Everyone who knows who wants to prove her ID will then compute (where c can be calculated as a hash of g, y and t):
\(t = g^r \times y^c\)
In this case the calculation gives 815,730,720, which is the same as the value of t that Alice sent, so they have proven her ID.
Every time Alice generates a new random number and proves that she knows the value of t each time.
Example
The following provides an example:
g= 3 x= 5555 y= 514769 p= 524287 ===== Peggy sends (t,r)=( 277645 , 95392 ) ===== Check: 277645 Peggy has proven she knows x
Code
An outline of the code used is:
import hashlib
g=3
p=2**19-1
x=5555
y=pow(g,x,p)
v=10553
t = pow(g,v,p)
chal = str(g) + str(y) + str(t)
h = hashlib.md5()
h.update(chal.encode("utf-8"))
c = int(h.hexdigest(), 16)
r = (v-c*x) % (p-1)
print ("g=",g)
print ("x=",x)
print ("y=",y)
print ("p=",p)
print ("=====")
print ('Peggy sends (t,r)=(',str(t),',',(r),')')
print ("=====")
check = (pow(g,r,p)*pow(y,c,p)) % p
print ("Check: ",check)
if (t==check):
print ("Peggy has proven she knows x")
else:
print ("Peggy has not proven she knows x")