Robots and Random Oracles: The Good and The Bad of Public Key Cryptography

Robots and Random Oracles: The Good and The Bad of Public Key Cryptography
We have a major problem with RSA public key encryption, and it focuses on the padding method used for the ciphered message. The main standard for formating an encrypted message is defined in PKCS (Public Key Cryptography Standards) #1. Overall there are two main methods: v1.5 and v2 (RSAES-OAEP). Unfortunately, the 1.5 standard — which was the first to be defined — but has been shown to be fairly easy to crack.
The main weakness of v1.5 is the Bleichenbacher’s attack [here] and which has been known about for over 20 years. It has been at the core of many attacks on SSL. It returned back in 2017 in the form of ROBOT (Return Of Bleichenbacher’s Oracle Threat https://robotattack.org/). The problem with v1.5 focuses on at the starting hex sequence of “00” “02” [RFC 2313]:

Optimal Asymmetric Encryption Padding (PKCS #1 v2)
Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with Enc=MessagePaddedᵉ(mod n) and decrypt with MessagePadded=Encᵈ(mod n). The padding is added before the encryption process, and then stripped off after decryption.
OAEP uses a Feistel network with a pair of random oracles G and H. These operator on the plaintext before it is encrypted. Its strengths are that it adds randomness to the process.
To encode [here]:
- The message is padded with with k1 zeros, and will be n − k0 bits in length.
- r is a random k0-bit string
- G expands the k0 bits of r to n − k0 bits.
- X = m00..0 ⊕ G(r)
- H reduces the n − k0 bits of X to k0 bits.
- Y = r ⊕ H(X)
- The output is X || Y where X is shown in the diagram as the leftmost block and Y as the rightmost block.
Where n is the number of bits in the RSA modulus (n), k0 and k1 are integers fixed by the protocol, m is the plaintext message which is an (n − k0 − k1)-bit string, G and H are hash functions, and ⊕ is an xor operation.
It is decoded with:
- Generate the random string as r = Y ⊕ H(X)
- Generate the message as m00..0 = X ⊕ G(r)
A sample run is:
Message: Hello
After padding: 0075d967552647f04b003b73f4c513d067de33dae1ba3a1e72714e63b7e795d36a72df6f1838dce2b4150fdf171e45c1b90988fe9329ee77861e5e6649d3181e2c8c032d8a501b64f1c72d01bda0b4ae1ef9bf36bc0e9f01236fd69b246850729e6ed26cf6513f02a5a826637861b836bcfd998cad48b2e812558f90add3bf63
Encrypted: 377c980ba36612bf4a1402d24cc7f10e08125d45521fca2179b2838eb8d1815b0d166b9ebfdc2e57d1253e0dd5de18b34d0913f5611e72335d23070fc8528cced4cb65eeec82b8539d1ef4573c101c92d91a56abe7bd6953f91bc86557d730a425dd39882e43ba27537d441cb00699d3d146bcec7c1b531c3725cb4121fa0c7b
Decrypted (before unpadding): 0x75d967552647f04b003b73f4c513d067de33dae1ba3a1e72714e63b7e795d36a72df6f1838dce2b4150fdf171e45c1b90988fe9329ee77861e5e6649d3181e2c8c032d8a501b64f1c72d01bda0b4ae1ef9bf36bc0e9f01236fd69b246850729e6ed26cf6513f02a5a826637861b836bcfd998cad48b2e812558f90add3bf63L
Decrypted: Hello
In this case we take the message, and then create a padded message. This message is raised to the power of e, and then the mod of n is taken. After this we can decrypt by raising this value to the power of d and taking of the mod of n. Next the padding is stripped off to give the original message.
An outline of the code is:
import math
import hashlib
from Crypto.Util.number import *
import sys
def RSAEnc(m, n, e):
return pow(m, e, n)
def RSADec(c, d, n):
return pow(c, d, n)
def HexstringToCharacters(hexstr):
clen = len(hexstr)
if clen & 1 == 1:
hexdata = hexstr[0]
outdata = chr(int(hexdata, 16))
c = 1
else:
outdata = ""
c = 0
for i in range(c, clen, 2):
hexdata = hexstr[i: i + 2]
outdata = outdata + chr(int(hexdata, 16))
return outdata
def FrmoCharacterToCode(arr):
outdata = ""
for i in range(len(arr)):
outdata = outdata + chr(arr[i])
return outdata
def MGF(seed, dLen):
dchar = HexstringToCharacters(seed)
c1 = int(math.floor(dLen * 1.0 / 20))
indata = dchar + FrmoCharacterToCode([0, 0, 0, 0])
outdata = int(hashlib.sha1(indata).hexdigest(), 16)
for i in range(1, c1 + 1):
indata = dchar + FrmoCharacterToCode([0, 0, 0, i])
indata = int(hashlib.sha1(indata).hexdigest(), 16)
outdata = outdata * pow(2, 160) + indata
outdata = outdata >> int((c1 + 1) * 160 - dLen * 8)
return hex(outdata)[2: int(2 * dLen + 2)]
def RSAOAEPEnc(m, mLen, n, e, r):
if mLen != len(m) / 2:
return False
k = int(math.ceil(size(n) / 8))
k2 = mLen
k0 = int(math.ceil(size(r) / 8))
k1 = k - 2 * k0 - k2 - 2
if k1 < 0:
return False
lhash = hashlib.sha1().hexdigest()
hLen = len(lhash) / 2
x01 = "01"
x00 = "00"
ps = []
while len(ps) != 2 * k1:
ps.append("0")
ps = "".join(ps)
pad = int(lhash + ps + x01 + m, 16)
s10 = int(MGF(hex(r)[2: len(hex(r)) - 1], k0 + k1 + k2 + 1), 16) ^ pad
s16 = hex(s10)[2: len(hex(s10)) - 1]
t10 = int(MGF(s16, k0), 16) ^ r
t16 = hex(t10)[2: len(hex(t10)) - 1]
w16 = x00 + t16 + s16
w10 = int(w16, 16)
str = hex(RSAEnc(w10, n, e))
return str[2: len(str) - 1]
def RSAOAEPDec(c, mLen, n, d, r):
k = int(math.ceil(size(n) / 8))
k0 = int(math.ceil(size(r) / 8))
k2 = mLen
k1 = k - 2 * k0 - k2 - 2
w10 = RSADec(int(c, 16), d, n)
s10 = (pow(2, 8 * (k0 + k1 + k2 + 1)) - 1) & w10
t10 = (pow(2, 8 * k0) - 1) & (w10 >> 8 * (k0 + k1 + k2 + 1))
rr = int(MGF(hex(s10)[2: len(hex(s10)) - 1], k0), 16) ^ t10
if r != rr:
return False
pad10 = int(MGF(hex(rr)[2: len(hex(rr)) - 1], k0 + k1 + k2 + 1), 16) ^ s10
pad = hex(pad10)[2: len(hex(pad10)) - 1]
m = (pow(2, 8 * k2) - 1) & pad10
lhash = (pow(2, 8 * k0) - 1) & pad10 >> 8 * (k1 + k2 + 1)
if hex(lhash)[2: len(hex(lhash)) - 1] != hashlib.sha1().hexdigest():
return False
return hex(m)[2: len(hex(m)) - 1]
msg="hello"
if (len(sys.argv)>1):
msg=str(sys.argv[1])
e=int("010001",16)
n=int("A9A4AFE96AF0B4F539B85FAD5F30D0B6C5394B73F672CB4BEF82A3D27349757DC33E925FECB0FCA4CC2219D90C4B8AA98CF5719BA79EB0AFEDA0FA6D42EEBA4F69562E6FF7015185B827FBAD264EBBC40984BD16273BDDB776E11169567BD3645D1A26656634A732F126B5E9044A5C88B9F6095AC874B0EA947BB35F48EBA4E7",16)
d=int("67A981F1016F0B34DA4B86F39B3A6A1F754EF88368F266B6052A704ED631EA40AA411F12CCC0ADF149E800A177F8E5478C222384F91D685C68B9B8AD717C0D8E2037B8582241F50FB893531396192A41F1643EEACABD5803CB74AE2D6CB38FE7A226CC5B0724DF0D0B4A50E592C7E25D7BA6A9A19CF940EE49715F1CEA2AD6A1",16)
r = 788255724614721016190591162463944054696650907899m=msg.encode("hex")mLen = len(m) / 2
enc= RSAOAEPEnc(m, mLen, n, e, r)
print "Message:\t",msg
print "Encrypted:\t",enc
m=RSAOAEPDec(enc, mLen, n, d, r)
print "Decrypted:\t",m.decode("hex")Bleichenbacher’s attack (PKCS #1 v1.5)
The Bleichenbacher’s attack [here] has been known for 20 years, and has been the core of many attacks on SSL. It returned back in 2017 in the form of ROBOT (Return Of Bleichenbacher’s Oracle Threat https://robotattack.org/).
A demo of the principles covered here is here.
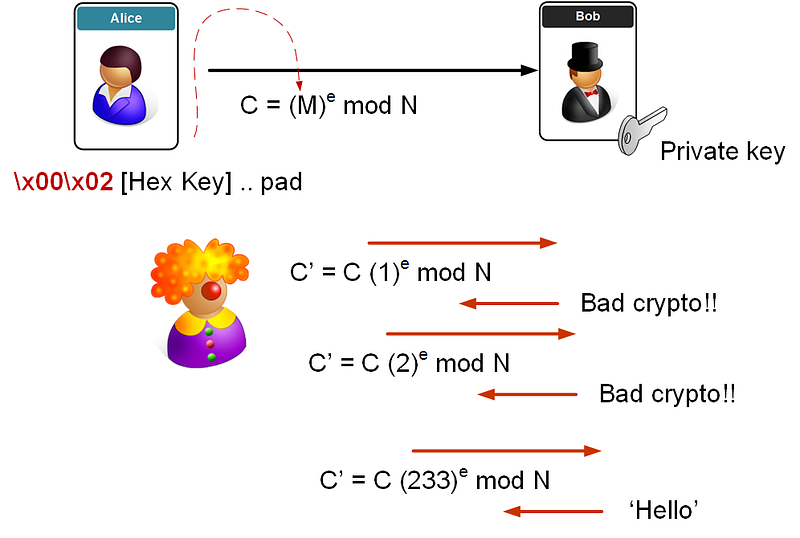
Let’s say that Eve is attacking the server. In the message she sends, there’s padding of the pre-shared key (as it is much smaller than the public modulus — n). In PKCS#1 v1.5 padding we then have two bytes at the start:
0x00 0x02
Eve then captures the cipher in the handshake and which contains the SSL pre-shared key (M):
C=M^e (mod N)
She then plays it back to the server, but adds an ‘s’ value (where she multiplies the cipher (C ) by s to the power of e (mod N)):
C′=C×(s^e) (mod N)
where e and N are the known public key elements. The server decrypts and gets:
M′=(C(s^e)) ^d (mod N)=C d×s^{ed} (mod N)=M×s (mod N)
M=C′s
When the server reads this, the first two bytes are likely to be incorrect, so it responds to say “Bad Crypto!”. Eve then keeps trying with different s values, until the server gives her a positive response, and she’s then on her way to finding the key. As we have 16 bits at the start, it will take us between 30,000 (1 in 215 which is 1-in-32,728) and 130,000 attempts (1 in 217 which is 1-in-131,073) to get a successful access.
We use padding to make sure that M (the pre-shared key) is the same length as the modulus (n). As M is only 48 bytes, we need to pad to give a length equal to n (256 bytes for a 2048-bit key).
In the end we just need to divide the original cipher by the value we have found, and we get M.
Coding
In this case we capture the cipher with M (which starts with \x00\x02), and then play it back with the addition of s^e, and then detect when there is a success in the cipher code:
import sys
e=79
d=1019
N=3337
def int_to_bytes(val, num_bytes):
return [(val & (0xff << pos*8)) >> pos*8 for pos in range(num_bytes)]
print '==Initial values ===='
print 'e=',e,'d=',d,'N=',N
print '\n============='
pad = '\x00\x02\x55\x55'
val = int(pad.encode('hex'), 16)
print 'Padding is:',pad,' Int:',valcipher = val**e % N
print 'Cipher is: ',cipher
for s in range(0,255):
cipher_dash = (cipher*(s**e)) % N
decode = cipher_dash **d % N
result = int_to_bytes(decode,2)
print s,
if (result[0]==0 and result[1]==2):
print '\n\\x00\\x02 Found it at s=',s
break
Key calculation
Let’s select:
P=47 Q=71
The calculation of n and PHI is:
n=P × Q = 13 × 11 = 3337
PHI = (p-1)(q-1) = 3220
We can select e as:
e = 79
Next we can calculate d from:
(79 × d) mod 3220 = 1 [Link]
d = 1019
Encryption key [3337,79]
Decryption key [3337,1019]
Then, with a message of 688, we get:
Cipher=(688)⁷⁹ mod 3337=1570
Decoded=(1570)¹⁰¹⁹ mod 3337=688
A sample run is [here]:
==Initial values ====
e= 79 d= 1019 N= 3337
=============
Padding is: �UU Int: 152917
Cipher is: 2652
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233
\x00\x02 Found it at s= 233
Conclusions
For PK’s sake … DO NOT USE PKCS #1 v1.5 … go check your server! You are in danger of losing your most precious of things … your private key.